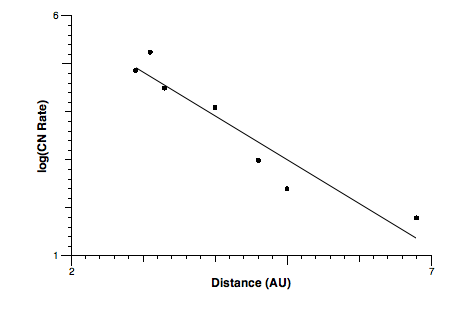
The response variable, y, is the rate of release of cyanide radical (CN) from the comet, measured in units proportional to molecules per second. The abscissa, x, is the comet's distance from the Sun in astronomical units (AU).
This is an example of a weighted least-squares regression [weighted R-squared = 0.99354]. The weights were known because the sensitivity of the measuring apparatus, etc. was known.
Had the weights been unknown, then there would have been no choice but to assume that the error variance was the same at all points. [Total ignorance is necessarily symmetrical.] In that case, the unweighted regression would have given the following parameter values:
[R-squared = 0.82936]
In scientific work, and elsewhere, it is often the parameter values that are of primary interest. This example shows that ignoring the fact that accuracy varies from point to point can sometimes produce large errors in parameter estimates.
It is easy to show that this assumption is incorrect (unless the points fall perfectly on the model curve). When we carry out the indicated transformation, using natural logarithms, and model the new dataset with a straight line, we get the following least-squares parameters:
Here is the corresponding graph:

R-squared is almost meaningless in this case because the whole model is invalid. It is not sufficient to equate these two models directly. Modeling the logarithm of y is clearly not the same as modeling y itself (with or without weights). The reason is that the transformation also modifies the residuals along the y-axis, and modifies some more than others. Standard regression algorithms ignore this fact. Transformations such as this can be done correctly, of course, but only if the residuals are treated properly.
For this reason, Regress+ never makes any nonlinear transformations, nor does it make approximations of any kind other than those inherent in sampling and bootstrapping generally.